由于内容过长、公式较多,暂时将内容隐藏,请公式恐惧症们做好心理准备。
题解备份Problem
Description
轮状病毒有很多变种,所有轮状病毒的变种都是从一个轮状基产生的。
一个
如下图所示
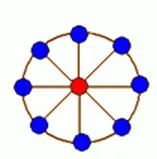
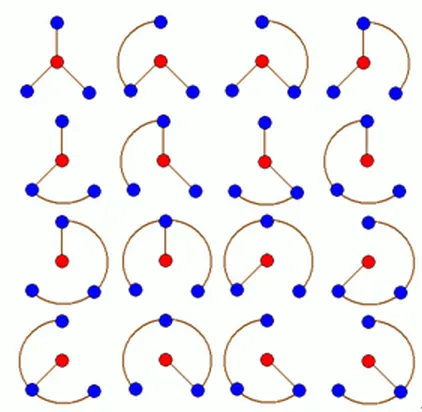
现给定
Input
第一行有
Output
计算出的不同的
Sample Input
3Sample Output
16法一: 行列式
转载自 vfleaking,
对于新手还是建议去看看基尔霍夫矩阵,这一篇论文挺不错的。
用基尔霍夫矩阵使用高斯消元解行列式,时间复杂度 AC。
首先行列式有很多性质:
- 第
- 三角行列式的值等于对角线元素之积
- 第
- 常数
如果你行列式不是很熟,建议先搜搜行列式~不然下面会看晕~
其实如果你仔细观察矩阵,可以发现它是这样的:(消去了病毒中央)
那么我们现在对行列式进行变换,我们把第
这个行列式跟一开始的那个行列式的值不一定相等。因为我们是通过
利用行列式性质,来手算这个行列式。之所以刚才有那么一步,就是为了方便手算。因为观察
这样就有了初步感觉了~
现在把这个过程一般化:
于是得到:
整合一下:
从初始的行和消了一次之后的行中取得边界条件:
好现在搞定了倒数第二行,来看看成果:
好,现在来搞倒数第一行。和倒数第二行的方法是类似的。
再设函数
其实跟
再来看成果:
用倒数第二行来消倒数第一行,得:
现在这个行列式已经是三角行列式了,它的值就是对角线元素之积。于是:
如前文所述:
又因为:
于是有:
带入
带入
然后再展开…… 回忆下
发现不能化简了?没关系!在行列式上动动手脚吧!
FH 定理
对于任意大于
证明:对于行列式:
把行列式最下面的行取反,则行列式的值取反:
把行列式的上面的行乘以
特意构造的递推式出现了:
有点眉目了~ 把第一行与第二行调换位置,行列式的值取反:
一目了然,这是 k++ 后的行列式的样子。(Pascal 同学早日转 C++)
那么立即推出:
FH 定理得证。
利用 FH 定理,把
于是就爽了嘛!
进一步我们发现…… 设
那么立即有:
所以,轮状病毒的方案数满足递推式
然后随手写一个高精度就可以过了~
法二:DP
转载自 boshi
如果用 f[x] 表示加入了
解释:最后加入的
但是,第一个点永远不会与第
我们再设:
解释:如果有
这样的
下面我们思考如何快速求出
多阶差分
首先分析
问题是对于不同的
那如果我们知道了变化的量是多少呢?于是我们就对前缀和进行差分。
我们维护
行列式解法:
#include <iostream>#include <cstdio>#include <cstring>#include <algorithm>#define digit 100000000using namespace std;struct bigint{ mutable int a[205]; inline bigint() { memset(a,0,sizeof(a)); a[0]=1;a[1]=0;return; } inline bigint(int b) { memset(a,0,sizeof(a)); a[0]=1;a[1]=b;return; } inline int& operator[](size_t pos)const{return a[pos];} inline bigint operator+(int b)const { int i;bigint c=*this; c[1]+=b; for(i=1;i<=c[0];++i) { if(c[i]>=digit) { ++c[i+1];c[i]-=digit; } } if(c[c[0]+1])++c[0]; return c; } inline bigint operator-(const bigint& b)const { int i;bigint c;c[0]=a[0]; for(i=1;i<=c[0];++i)c[i]=a[i]-b[i]; for(i=1;i<=c[0];++i) { if(c[i]<0) { c[i]+=digit;--c[i+1]; } } while(!c[c[0]]&&c[0]>1)--c[0]; return c; } inline bigint operator*(int b)const { int i;bigint c;c[0]=a[0]; for(i=1;i<=c[0];++i)c[i]=a[i]*b; for(i=1;i<=c[0]||c[i];++i) { if(c[i]>=digit) { c[i+1]+=c[i]/digit;c[i]%=digit; } } c[0]=i-1; return c; } friend ostream& operator<<(ostream& os,const bigint& a) { printf("%d",a[a[0]]); for(int i=a[0]-1;i>=1;--i)printf("%08d",a[i]); return os; }}f[3005];int main(void){ int i,n; scanf("%d",&n); f[1]=1;f[2]=5; for(i=3;i<=n;++i)f[i]=f[i-1]*3-f[i-2]+2; cout<<f[n]<<endl; return 0;}DP 解法:
#include <iostream>#include <cstdio>#include <cstring>#include <algorithm>#define digit 1000000000using namespace std;struct bigint{ mutable int a[205]; inline bigint() { memset(a,0,sizeof(a)); a[0]=1;a[1]=0;return; } inline bigint(int b) { memset(a,0,sizeof(a)); a[0]=1;a[1]=b;return; } inline int& operator[](size_t pos)const{return a[pos];} inline bigint& operator+=(const bigint& b) { int i;a[0]=max(a[0],b[0]); for(i=1;i<=a[0];++i)a[i]+=b[i]; for(i=1;i<=a[0];++i) { if(a[i]>=digit) { ++a[i+1];a[i]-=digit; } } if(a[a[0]+1])++a[0]; return *this; } friend ostream& operator<<(ostream& os,const bigint& a) { printf("%d",a[a[0]]); for(int i=a[0]-1;i>=1;--i)printf("%09d",a[i]); return os; }}F=1,F1=1,F2=1,G=0,G1=0,G2=0;int main(void){ int i,n; scanf("%d",&n); for(i=1;i<=n;++i) { if(i)G2+=F,G2+=F; if(i<n)G1+=G2,G+=G1; F=F1;F2+=F;F1+=F2; } cout<<(F+=G)<<endl; return 0;}完结撒花!★,°:.☆( ̄▽ ̄)/$:.°★